1. logistic分类
几乎所有的教材都是从logistic分类开始的,因为logistic分类实在太经典,而且是神经网络的基本组成部分,每个神经元(cell)都可以看做是进行了一次logistic分类。
所谓logistic分类,顾名思义,逻辑分类,是一种二分类法,能将数据分成0和1两类。
logistic分类的流程比较简单,主要有线性求和,sigmoid函数激活,计算误差,修正参数这4个步骤。前两部用于判断,后两步用于修正。本文分为3部分,前2部分讲普通logistic分类的流程,第三部分则稍作扩展。
它的优点一是逻辑回归的算法已经比较成熟,预测较为准确;二是模型求出的系数易于理解,便于解释,不属于黑盒模型,尤其在银行业,80%的预测是使用逻辑回归;三是结果是概率值,可以做ranking model;四是训练快。当然它也有缺点,分类较多的y都不是很适用;对于自变量的多重共线性比较敏感,所以需要利用因子分析或聚类分析来选择代表性的自变量;另外预测结果呈现S型,两端概率变化小,中间概率变化大比较敏感,导致很多区间的变量的变化对目标概率的影响没有区分度,无法确定阈值。
1.1 线性求和以及sigmoid函数
第1,2步是用于根据输入来判断分类的,所以放在一起说。假设有一个n维的输入列向量 x,也有一个n维的参数列向量h, 还有一个偏置量b, 那么就可以线性求和得到z.

此时因为z的值域是[−∞,+∞] ,是无法根据z来判断x 到底是属于0还是1的。因此我们需要一个函数,来将z的值映射到[0,1]之间, 这就是激活函数。激活函数有很多种,这里的激活函数是sigmoid函数。

其形状为
 图1 sigmoid函数
图1 sigmoid函数 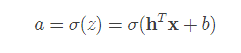 当 a 大于0.5的时候,我们判定x应属于1类,如果小于0.5,则属于0类。这样,就完成了判断的工作。
当 a 大于0.5的时候,我们判定x应属于1类,如果小于0.5,则属于0类。这样,就完成了判断的工作。
损失函数是在机器学习中最常出现的概念,用于衡量均方误差[(模型估计值-模型实际值)^2/ n]最小,即预测的准确性,因而需要损失函数最小,得到的参数才最优。(线性回归中的最小二乘估计也是由此而来)但因为逻辑回归的这种损失函数非凸,不能找到全局最低点。因此,需要采用另一种方式,将其转化为求最大似然,如下,具体的推导求解过程可参见博客 另一种较为好理解的方式是,如果Y=1,你胆敢给出一个h(x)很小的概率比如0.01,那么损失函数就会变得很大:
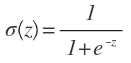

1.2 误差计算以及参数修正
上面完成的判断过程中用到了参数向量h和偏置量b。 可以说,h和b的值直接关系到logistic判断的准确性。那么这两组参数是如何获得的呢?这就涉及到了参数的修正。在最开始的时候,h中的值是随机的,而b的值是0. 我们通过不断的训练来使得h和b能够尽可能的达到一个较优的值。
那么如何训练呢?假设我们期望输入x的判定是y,而实际得到的判定值是a,那么我们定义一个损失函数C(a,y),通过修正h和b的值来使得C最小化,这是一个优化问题。在凸优化问题中,可以通过
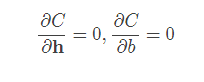
来直接算得h和b的最优解。然而在某些情况下,例如数据规模很大,或者非凸优化问题中,则不能这么做,而是用迭代的方法来得到局部最优解。

其中 η 表示学习率。在这里,我们把损失函数定为平方损失函数,即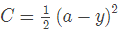 那么可以得到
那么可以得到

这样,就能够得到每次迭代的参数更新公式为
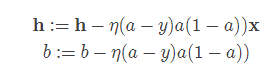
1.3 将logistic扩展到多分类
从之前可以看出,普通的logistic只能进行二分类,即只能够分为0或者1。那么如果这些样本属于多个类该怎么办呢?人们想了很多办法,例如一对多法,依次把某个类别的样本归为一类,其他剩余的样本归为另一类,这样k个类需要构建k个分类器。还有一对一法,在任意两类样本之间设计一个分类器,k个类需要k(k-1)/2个分类器。
在这里,我们将输出由一个值更改为一个向量。例如有3个类,那么输出就是一个长度为3 的列向量,对应项的值为1,其他为0.即
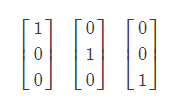 分别表示第0,1,2个类。 也可以看成是原来若干个logistic分类器组合在一起。对应的某个分类器只对该类输出1,其他情况都输出0.从这一点上来讲,这个做法有点类似于一对多法。此时,由于输出从一个数成为一个向量,之前的公式都要加以修改。首先,原来的y,a,z,b变成了列向量, 向量h变成了矩阵W。这样,判断部分的公式变为
分别表示第0,1,2个类。 也可以看成是原来若干个logistic分类器组合在一起。对应的某个分类器只对该类输出1,其他情况都输出0.从这一点上来讲,这个做法有点类似于一对多法。此时,由于输出从一个数成为一个向量,之前的公式都要加以修改。首先,原来的y,a,z,b变成了列向量, 向量h变成了矩阵W。这样,判断部分的公式变为

此时的σ函数表示对向量中的每一个元素单独做运算。即
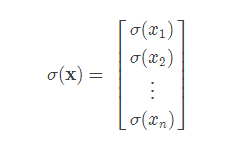
得到的a向量中,其最大值所在的位置索引即为判断出的分类。 参数修正部分的公式也是类似的,
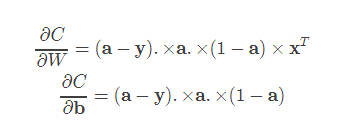
注意有些向量之间是进行.
转自:http://blog.csdn.net/u014595019/article/details/52554582